|
IL DIPOLO
Da diverso tempo desideravo realizzare un sistema a dipolo ma, come al solito, volevo mettere qualcosa di mio nel progetto, quindi fare semplicemente un buco in un pannello e ficcarci un altoparlante non mi bastava. Così sono andato avanti nell’analisi del sistema, alla ricerca delle migliori soluzioni.
LA TEORIA DI BASE DEL DIPOLO CLASSICO
Partiamo dalla base, quella che tutti conoscono: il pannello costituisce uno schermo acustico tra l’emissione anteriore e quella posteriore di un altoparlante (che è in controfase), ed è efficace fino a che la sua larghezza risulta pari a metà della lunghezza d’onda ( ). Questa corrisponde quindi alla frequenza di taglio del pannello o Ft. Per determinare la larghezza del pannello è allora sufficiente dividere la velocità del suono (344 m/s), per la Ft desiderata, tovando ). Questa corrisponde quindi alla frequenza di taglio del pannello o Ft. Per determinare la larghezza del pannello è allora sufficiente dividere la velocità del suono (344 m/s), per la Ft desiderata, tovando  , e poi dividere ancora per 2 : , e poi dividere ancora per 2 :
quindi, se volessimo una Ft di 100 Hz:
Ft 100 Hz = (344/Ft)/2 = 3.44/2 =1,72 (metri)
Un pannello largo 1,72 metri è un bel pannello, non c’è che dire... Per fortuna la presenza del pavimento crea una immagine “specchio” (mirror image), che fa apparire tale misura aumentata per un fattore uguale alla radice quadrata di 2, (1,41 per comodità) quindi 1,72 metri verrebbero visti dal sistema come 1,72*1,41,cioè 2,425, mentre, bastando a noi 1,72 metri, possiamo ridurre il dato iniziale sempre per radice di 2, quindi
D = (1,72/1,41) = 1,22 (circa, lo so, non fate i pignoli!)
dove D = dimensione pannello

La tabella sopra permette di calcolare approssimativamente il semipannello relativo alla frequenza di taglio scelta, senza calcolare l'incremento dovuto al pavimento. si ottiene quindi la distanza tra il centro dell'altoparlante e il bordo del pannello. Nel nostro caso, per una Ft di 100 hz, possiamo leggere circa 32,5 pollici, poiché 1 pollice = 2,54 cm, abbiamo 82,5 cm che, moltiplicati per 2, danno 165 cm, contro i 172 cm da noi calcolati. Dato che non conosciamo il dato di C utilizzato dal compilatore della tabella, la tolleranza potrebbe anche essere minore.
Se volessimo ridurre ulteriormente le dimensioni, potremo ripiegare in parte i bordi del pannello (al massimo il 1/6 della D per ogni lato, come consiglia Olson quando parla dei diffusori “open back”) togliendo altri 20 centimetri per lato, e scendendo ben sotto il metro.
Un metro è pur sempre un metro, direte voi, e 100Hz sono comunque tanti per potersi immaginare dei bassi profondi....
Nella realtà le cose sono meno tragiche di quanto possa sembrare a prima vista: un dipolo inizia a perdere efficacia alla Ft, quindi nella pratica un sistema dimensionato come ipotizzato sopra dovrebbe essere “flat” fino a 100 Hz, quindi la risposta dovrebbe scendere al ritmo di 6 dB ott. fino alla Fs dell’altoparlante (questa è la “perdita” dovuta al pannello), per poi precipitare con una pendenza di 18 dB ott. (e questa è la somma della pendenza del pannello sommata alla pendenza caratteristica di un altoparlante al disotto della Fs, che è intorno ai 12 dB ott.)
Alla luce di questo si può quindi immaginare che un altoparlante con Fs di 25Hz vedrebbe un punto a meno 12 dB ( due ottave sotto i 100Hz) proprio a questa frequenza, che è un bel limite, a dispetto della Ft relativamente alta, e perderebbe poi 18 dB fino ai 12,5 Hz, dove siamo già all’infrasuono.
Quindi la situazione non è assolutamente comparabile con un sistema tradizionale, che sotto la Ft vede un rapido calo dell’energia, mediamente da 12 a 18 db ott., con quella brutta sensazione di basso troncato tipica di certi sistemi accordati ad alta pendenza.
FATTORI POCO CONSIDERATI NEL DIPOLO CLASSICO
Per prima cosa bisogna precisare che la teoria vista prima è valida (in linea di massima) solo se l’altoparlante ha un Qt di 1 (e qualcosa in più non guasterebbe, dico io): valori di Qt inferiori avranno una risposta molto meno estesa, viziata dal maggiore smorzamento in bassa frequenza. Questa caratteristica è ben illustrata da Small quando definisce le curve caratteristiche relative ai fattori di merito totale (Qt): per avere la massima pressione possibile fino alla Fs si deve avere un Qt di almeno 1. Cosa poi ribadita analizzando i sistemi in cassa chiusa, il cui PAR, (Acoustic Power Rating), o massima efficienza acustica, viene raggiunta con un Qt di 1,1, come risulta dalla curva di Kp, o costante di potenza, plottata in funzione del Qtc del sistema.

Utilizzando Qt superiori sarebbe invece possibile sfruttare il maggior livello alla risonanza per compensare il calo dovuto alla ridotta larghezza del pannello. Questa possibilità, per esempio, è stata sfruttata da Jim Croft, che progettò per la Carver l’“Amazing loudspeakers”, sistema dipolare che usava un array di alcuni woofer “free air” ad alto Qt da 12 pollici. Questo tipo di realizzazione comporta però l’utilizzo di altoparlanti particolari, quasi impossibili da trovare in commercio.

Il reale andamento della curva di pressione di un dipolo è illustrata con chiarezza da Olson (sopra) in un paper AES sugli altoparlanti a gradiente, ove un altoparlante è assimilato a un trasduttore a gradiente bidirezionale del primo ordine, e la risposta plottata sull’asse mostra un andamento caratteristico per le varie distanze in funzione di D/ , e ci fornisce anche una risposta polare sull’asse orizzontale, che ci aiuta a comprendere una peculiarità del dipolo, illustrata anche da Linkwiz, che consiste in uno slittamento del punto di massima energia per angolazioni prossime ai 60° alla frequenza pari a D/ , e ci fornisce anche una risposta polare sull’asse orizzontale, che ci aiuta a comprendere una peculiarità del dipolo, illustrata anche da Linkwiz, che consiste in uno slittamento del punto di massima energia per angolazioni prossime ai 60° alla frequenza pari a D/ =1. Questo comporta un riempimento energetico del buco presente sull’asse alla stessa frequenza, con un comportamento più lineare del calcolato in caso di posizionamento in ambiente. =1. Questo comporta un riempimento energetico del buco presente sull’asse alla stessa frequenza, con un comportamento più lineare del calcolato in caso di posizionamento in ambiente.
Dagli stessi articoli deduciamo anche altre cose:
1- la Ft (o Fc, stessa cosa) o frequenza di taglio, è in effetti da considerare come il punto a +3dB, dato che esiste un incremento di emissione a Ft dovuto al fatto che alla stessa frequenza in cui inizia il calo di 6 dB ott. la lunghezza d’onda inizia ad essere comparabile con la larghezza del pannello e tale per cui le emissioni anteriore e posteriore si trovano in fase, (D/ =0,5) quindi la transizione al regime “flat” sarà caratterizzato da un picco di alcuni dB (3 in teoria) rispetto alla pressione massima calcolabile, quindi per confrontare l’estensione in basso di un dipolo con altri sistemi, dovremo fare riferimento a Ft/2, essendo questo il punto a -3dB, normalmente usato per definire la minima frequenza nei sistemi tradizionali. =0,5) quindi la transizione al regime “flat” sarà caratterizzato da un picco di alcuni dB (3 in teoria) rispetto alla pressione massima calcolabile, quindi per confrontare l’estensione in basso di un dipolo con altri sistemi, dovremo fare riferimento a Ft/2, essendo questo il punto a -3dB, normalmente usato per definire la minima frequenza nei sistemi tradizionali.
Alla frequenza doppia dovremmo poi avere un calo di energia, (teoricamente un buco, ma abbiamo visto che la caratteristica polare compensa tale difetto) ma ricordiamoci anche che, se riduciamo la larghezza del pannello di un fattore 1.41, la 2Ft (D/ =1) potrebbe non essere esattamente il doppio della frequenza calcolata come Ft (per la quale abbiamo ipotizzato una larghezza fittizia), ma superiore, dato che l’effetto “mirror” del pavimento potrebbe essere meno sentito dalle frequenze superiori, più sensibili alla larghezza fisica del pannello. =1) potrebbe non essere esattamente il doppio della frequenza calcolata come Ft (per la quale abbiamo ipotizzato una larghezza fittizia), ma superiore, dato che l’effetto “mirror” del pavimento potrebbe essere meno sentito dalle frequenze superiori, più sensibili alla larghezza fisica del pannello.

2 - Per gli stessi motivi di cui sopra, alle frequenze multiple dispari di Ft avremo dei picchi di pressione, mentre ai multipli pari avremo buchi dovuti alle interazioni di fase (vedi grafico sopra).

3 - La polare di un dipolo è in effetti da considerare vincolata alla dispersione caratteristica dell’altoparlante impiegato. Se un altoparlante non emette energia a 90°, la cancellazione di fase dovuta alla lunghezza dello schermo acustico non avverrà; questo comporta il fatto che l’utilizzo di altoparlanti in qualche modo controllati nella dispersione comporta meno problemi nell’uso a dipolo. Dato che la dispersione è in funzione del diametro del pistone radiante, man mano che si sale in frequenza l’energia emessa fuori asse da un altoparlante cala, e ciò spiega la sostanziale maggior linearità del dipolo alle frequenze superiori ove, se si volesse seguire la regola dei “buchi” ai multipli pari di Ft, si dovrebbe avere una risposta “a pettine” abbastanza tormentata. Facendo riferimento al grafico della potenza acustica irradiata in funzione del diametro del pistone (sopra), si scopre poi che scegliendo opportunamente il diametro del trasduttore, il dipolo è in taluni casi più efficiente del monopolo. Infatti un pistone diviene direttivo quando d/ =0,32 (Keele indica 0,26, o fattore k*a=1,6 dove k=2 =0,32 (Keele indica 0,26, o fattore k*a=1,6 dove k=2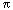 / / e a=raggio del pistone), mentre il dipolo assume la medesima caratteristica direzionale a d/ e a=raggio del pistone), mentre il dipolo assume la medesima caratteristica direzionale a d/ =0,86. Questa particolarità risulterà molto evidente in sede di misura di un prototipo, dato che la canonica distanza di 1 metro rende l’emissione catturata dal microfono troppo simile ad un monopolo, mentre se si sposta il punto di misura in una zona influenzata dal campo riverberato, l’energia acustica sarà inaspettatamente maggiore nell’area interessata. =0,86. Questa particolarità risulterà molto evidente in sede di misura di un prototipo, dato che la canonica distanza di 1 metro rende l’emissione catturata dal microfono troppo simile ad un monopolo, mentre se si sposta il punto di misura in una zona influenzata dal campo riverberato, l’energia acustica sarà inaspettatamente maggiore nell’area interessata.

4 - Bisogna considerare che il pannello costituisce anche un carico acustico che condiziona la transizione da un semispazio allo spazio intero della radiazione diretta, e la cosa comporta un incremento di emissione che inizia alla frequenza la cui lunghezza d’onda è pari a C/5D ovvero la velocità del suono fratto 5 volte la misura del pannello, e finisce a C/2D, quindi, nel caso prima ipotizzato, con un pannello da 1,22 m (attenzione, non di 1,72!) avremo un incremento di emissione che parte a circa 56 Hz e termina a 140 Hz. Questo incremento si va a sovrapporre alla risposta del dipolo e, guarda che caso (!) proprio a cavallo tra la regione “flat“ e il tratto in calando a 6 dB ottava. Raramente ho visto puntualizzare questo fatto, addirittura Linkwitz, illustrando il suo progetto Phoenix (grafico sopra, freccia in alto a sinistra), si accorge di questo comportamento anomalo, ma attribuisce l’aumento dell’emissione in questa regione a un problema del cestello dell’altoparlante e Raymond Newman, in un interessantissimo studio pubblicato nel 1980, azzarda l’ipotesi che il rinforzo “inaspettato” tra i 100 e i 400 Hz del suo dipolo sia dovuto alla congiunzione col pavimento, che porta il sistema a irradiare su 1/4 di spazio ma “...this is only conjecture” che, ovviamente è superfluo tradurre: in effetti l’incremento si sposta molto in frequenza rispetto ai calcoli, quindi Newman ha sicuramente ragione e vedremo che questo ragionamento ci tornerà comunque utile... Anche il dipolo Res-Audax di Daniele Coen, presentato su AudioReview n°150, mostra un comportamento altalenante in corrispondenza della zona di transizione e, dato che il pannello è largo 40 cm, l’incremento dovuto allo stesso dovrebbe essere compreso tra circa 172 e 430 Hz, e così pare di notare nell’unico grafico a disposizione, realizzato in ambiente. Tra l’altro Coen fa un accenno a un particolare “accorgimento acustico”, di cui ha richiesto il brevetto, per linearizzare la risposta. Non ho idea di cosa si tratti dato che non mi pare sia stato dato un seguito a quell’articolo né Coen abbia pubblicizzato in qualche modo detto dispositivo; la curiosità rimane...
L’EFFICIENZA IN BASSA FREQUENZA DI UN DIPOLO
Il ragionamento che sta alla base della determinazione del dato di efficienza del dipolo è abbastanza semplice, e parte dall’esame della formula che ci fornisce l’efficienza di drasduzione (h) o la potenza acustica (Pa) di un dato altoparlante. Questi valori sono espressi in percentuale o in Watt e possono poi essere convertiti in decibel (dBspl). Per quanto ci riguarda possiamo mantenere i valori originali, dato che lo scopo dell’indagine non è quello di determinare i dBspl prodotti da un dato altoparlante, quanto verificare quali parametri influenzino l’efficienza di trasduzione di un altoparlante montato su un pannello finito. Questo è un punto importante, dato che il dato di efficienza comunemente usato per definire i monopoli, cassa chiusa o reflex che sia, non è applicabile al dipolo, per il quale è più corretto usare la formula data per definire la potenza acustica irradiata da un pistone in aria libera, non essendo il trasduttore influenzato da un volume di carico. Quando si ricercano dati del genere è facile imbattersi in un mare di formule, più che in una unica soluzione: ad esempio, gli studi di Small e Thiele tengono spesso conto del “sistema altoparlante”, comprendendo con ciò il volume di carico dello stesso, o la somma dei trasduttori installati più l’eventuale porta reflex ecc.... , mentre nel nostro caso vengono più utili gli studi di Keele, che analizzano a fondo il comportamento in bassa frequenza degli altoparlanti, sia in campo vicino che in campo lontano. Alla fine si tratta di diverse stesure delle stesse formule e i concetti rimangono gli stessi, sembra quasi che tutti si siano divertiti a scombinare le carte per dire la propria a proprio modo... Comunque sia ho trovato i diversi calcoli che definiscono una tale situazione e ve li ripropongo:
Partiamo dalle origini, cioè gli studi di Rice e Kellogs del 1925, alla base dello sviluppo del moderno altoparlante elettrodinamico a radiazione diretta. In questa ricerca ci si riferisce a Rayleigh nella parte che definisce P la potenza irradiata da una singola faccia di un “piccolo diaframma”, dove per piccolo si intende un diaframma con diametro inferiore alla lunghezza d’onda da trattare, quindi un classico altoparlante per basse frequenze (per intenderci, i 100 Hz hanno una lunghezza d’onda di circa 3,5 metri e altoparlanti di tale diametro esistono solo al cinema, ricordate “Ritorno al futuro”?).
diaframma che, nel caso sia montato su un pannello, irradia su un semispazio, cioè 2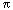 : :
P= p/(S2*w4*X2)/2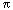 v v
dove
p= densità dell’aria in g/cm3 (o 1,18 Kg/m3)
v= velocità del suono (344 cm/s)
S= area del diaframma
w= 2*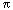 *ƒ *ƒ
X= ampiezza dell’escursione del diaframma
Andiamo avanti negli anni e arriviamo a Keele e Small, negli anni 70: tralasciando le ricerche sui sistemi chiusi, ci concentriamo sui parametri caratteristici degli altoparlanti, dove troviamo la definizione di efficienza caratteristica h
La formula precedente viene confermata da Keele nei suoi studi sulle misurazioni di pressione acustica in campo vicino:
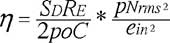
dove
SD = superficie radiante
RE = resistenza in continua della bobina mobile
po = densità dell’aria (qui fissata 1,21 Kg/m3)
pNrms = pressione di picco media in campo vicino del pistone
ein = voltaggio applicato all’ingresso dell’altoparlante
Da ciò si comincia a dedurre che, a parità di costanti (velocità del suono, densità dell’aria, escursione del diaframma, Re della bobina, tensione applicata e frequenza in esame) un pistone di grosse dimensioni e con grossa escursione è più efficiente di uno piccolo e con poca escursione, infatti modificando anche solo una di queste variabili il dato di efficienza viene incrementato.
Andando a Small, troviamo invece la seguente formula:

(attenzione, la costante 9,6*10-7 deriva da 4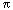 2/C3 e vale se si calcola la Fs in Hz e la Vas in metri cubi, ma diventa 9,6*10-10 se la Vas è espressa in litri e 9,6*10-8 se la Vas è espressa in piedi cubici) 2/C3 e vale se si calcola la Fs in Hz e la Vas in metri cubi, ma diventa 9,6*10-10 se la Vas è espressa in litri e 9,6*10-8 se la Vas è espressa in piedi cubici)
Qui osserviamo un’altra cosa, cioè che per aumentare l’efficienza di trasduzione è possibile aumentare la Vas, cioè il volume di aria avente la stessa cedevolezza acustica delle sospensioni dell’altoparlante.

Un ragionamento di Newman, tratto dal già citato articolo, evidenziava come la Vas fosse un fattore determinante per l’efficienza di un altoparlante. La cosa non mi era ben chiara fino a quando non mi sono imbattuto in un articolo curioso in cui veniva mostrato un array di woofer senza pannello, illustrato a fianco. Le risposte in frequenza misurate con 1, 2 o 4 woofer collegati mostravano una cosa interessante: la curva di pressione non veniva traslata in livello in modo eguale per tutte le frequenze come avrei potuto immaginare, ma vi era un incremento lato basse frequenze dovuto al solo aumento del dato di Vas, che veniva raddoppiato o quadruplicato.
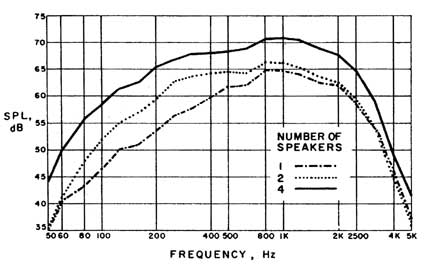
Ovviamente i woofer erano identici. Infatti l’altro parametro che avrebbe potuto influenzare la risposta in frequenza era il Qt, ma questo dato non cambia per qualsiasi tipologia di connessione elettrica, sia essa serie o parallelo o mista, idem per l’escursione, che rimane identica, mentre l’incremento in livello è normalmente dato dall’aumento della superficie radiante e/o dal dimezzamento del carico visto dall’amplificatore. Ma avevo sempre pensato che detto aumento dovesse essere uguale per tutte le frequenze, mentre qui si metteva chiaramente in evidenza che il solo aumento del Vas porta ad una maggiore efficienza del sistema in bassa frequenza. In pratica a parità di altri parametri da ritenere tipici per determinare l’efficienza in bassa frequenza di un altoparlante da utilizzare in dipolo, quali il Qt e la Sd, bisogna dare la massima importanza al Vas.
Altro fattore importante, e legato a quanto visto prima, è il dato di VD o volume d’aria spostato dalla massima escursione dell’altoparlante e dato dalla formula
VD = SD*Xmax
dove
SD = superficie radiante
Xmax = massima escursione del cono
Se torniamo al dato del PAR, o Acoustic Power Rating, già visto in occasione del ragionamento fatto a proposito del Q ideale per ottenere la massima effficienza, troviamo i seguenti dati:
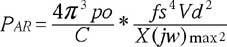
Da ciò deduciamo che la potenza acustica irradiata da un sistema è strettamente legata alla relazione tra la Fs (frequenza di risonanza) e il VD, fratto X(jw)max, cioè il valore normalizzato dalla funzione di escursione relativo al Qt dell’altoparlante, quindi, oltre a scegliere un determinato Qt, è bene che anche la Xmax sia la più alta possibile, pena una impossibilità a generare il necessario Vd.
A questo punto resta da analizzare solo l’escursione cui può essere sottoposto un altoparlante non controllato da un volume d’aria retrostante, sia esso chiuso o accordato. Per questo ci riferiamo a Small (JAES Vol. 20 n°5 1972), che definisce il PER o Displacement-Limited Electrical Power Rating, o potenza elettrica limitata dall’escursione massima dell’altoparlante:
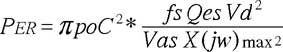
Small dimostra come un altoparlante ad alta cedevolezza ha una bassa capacità di accettare potenza in ingresso, dato che raggiunge più velocemente il dato di Xmax, o massima escursione dell’equipaggio mobile. In pratica, (ma la cosa è chiara anche osservando la formula di Rayleigh vista in precedenza), bisogna ricercare un alto valore di Xmax se si desidera efficienza in bassa frequenza, ma un basso valore di Cms o cedevolezza dell’equipaggio mobile, se non si vuole superare il massimo dato di escursione anche con potenze modeste in ingresso. Questo parametro è abbastanza critico quando si ha a che fare con altoparlanti ad alto Q e bassa Fs, dato che il PER è direttamente legata alla frequenza da riprodurre, alla tensione in ingresso, alla cedevolezza, alla massa mobile Mas e al fattore di forza o Bl, che negli altoparlanti ad alto Q è per forza di cose basso.
Infatti: Vas=po*C2*Cas, e Cas è la cedevolezza acustica delle sospensioni dell’altoparlante, direttamente correlata col dato di Cms, o cedevolezza meccanica delle sospensioni, dato che Cms=Cas*Sd2, mentre il Qes, o fattore di merito elettrico, è funzione di Fs e Bl: Qes=ws*Re*Mas*Sd2/(B2l2)
Insomma, un sottile equilibrio lega le caratteristiche elettromeccaniche di un altoparlante, e questo spiega la infinità di possibili varianti e la specifica destinazione d’uso di ciascuno di essi.
Il legame diretto tra tutti questi fattori è illustrato molto bene in uno studio di Jason Christophorou, che riguarda le misure in bassa frequenza degli altoparlanti per mezzo di un accelerometro.
PER CONCLUDERE
Per fare un dipolo con una efficienza decente in bassa frequenza si deve dimensionare il pannello in modo adeguato e scegliere un woofer con Qt prossimo a 1, ma che volete fare, un pannello di 2 metri per due? A voi la scelta, a me un metro pare già troppo...
OLTRE IL DIPOLO?
Abbiamo visto che tipo di scelte bisogna fare per ottenere il massimo da un dipolo.
Adesso però poniamoci un quesito:
Domanda: in che condizioni si verificano le cancellazioni e alterazioni nella risposta?
Risposta: allorquando le emissioni anteriore e posteriore siano identiche in livello e frequenza ma in opposizione di fase.
Ovvio che se ci discosta da questi presupposti l’andamento teorico viene modificato.
Bene, a parte il fatto che un altoparlante non emette in modo identico sulle due facce, quantomeno perchè sul retro esiste uno schermo acustico formato da cestello e magnete, diamo per buona la condizione di eguaglianza d’emissione in frequenza e livello; e pure, ovviamente, l’opposizione di fase nell’emissione delle facce opposte della membrana di un comune altoparlante.
In questo modo siamo in presenza di una condizione ideale.
Ma cosa succederebbe se alla fine del pannello (o semipannello) si incontrassero due emissioni di fase opposta ma di livello non eguale? La cancellazione non sarà perfetta e l’attenuazione prevista risulterà minore.
La cosa è peraltro ovvia: una cassa chiusa costituisce l’estremo della cosa, con la totale cancellazione dell’emissione posteriore e nessuna cancellazione di fase.
Per alterare questo dato di fatto dobbiamo allora intervenire su qualche parametro dell’altoparlante.
Dato che il trasduttore è uno, sarà unico il magnete (e il Bl non sarà modificabile, quindi il Qt non può variare se non inserendo resistenze elettriche o acustiche) sarà unica la membrana (quindi anche la Mms) e unica la bobina (e la Re), quindi non si può, per esempio, far suonare più forte una sola faccia del dipolo, questo stratagemma lo si raggiunge coibentando pesantemente la faccia posteriore dell’altoparlante e trasformando il caratteristico lobo del dipolo in un qualcosa di simile al cardioide microfonico, ma questa pratica abbassa anche il Qt. Sarebbero unici anche la superficie radiante e il Vas se non si riuscisse a modificare almeno questi dati in qualche modo.
Questo modo di procedere è peraltro conosciuto e trattato anche in alcuni Journal dell’AES, ma le soluzioni proposte per diversificare le superfici radianti delle due facce del dipolo sono alquanto macchinose. Il dipolo di Shearer, realizzato negli anni 30 per sonorizzazione cinematografica, aveva la faccia anteriore dell’altoparlante caricata a tromba, ottenendo così contemporaneamente due risultati: le pareti della tromba fungevano da pannello schermo e la tromba accoppiava la sola radiazione anteriore della membrana all’ambiente, realizzando un incremento della superficie radiante della stessa. Questo sistema è stato anche analizzato da Hilliard (JAES vol. 26 del 1978).
La cosa viene anche confermata da Baranek, che ci dice che la resistenza di radiazione di un diaframma operante in bassa frequenza è:
1.57*w2*a4*Po/C
dove
w= 2*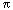 *ƒ *ƒ
a = raggio del diaframma in metri
Po = densità dell’aria
C = velocità del suono
Quindi basta semplicemente aumentare la superficie radiante di una sola delle facce per ottenere il risultato voluto, e la tromba ottiene questo scopo.
Ora bisogna convenire che la realizzazione di una tromba per basse frequenze risulta complessa e porta necessariamente a ingombri notevoli.
Bisogna quindi pensare a qualche altra soluzione.
Se non vogliamo o possiamo incrementare la Sd della faccia anteriore dell’altoparlante, possiamo sempre cercare di ridurla dall’altro lato, e il risultato non cambierebbe.
Quindi se noi riuscissimo a parzializzare la superficie radiante posteriore, la sensibilità dell’altoparlante in quella parte diminuirà di conseguenza e il risultato verrebbe in qualche modo raggiunto.
Un metodo potrebbe essere quello di separare fisicamente in due la membrana nella parte posteriore, e ciò si può fare interponendo una paratia che, seguendo la forma del cestello e gruppo magnetico, separi in verticale il diametro dell’altoparlante in due porzioni uguali.
Quindi montando su un classico dipolo una paratia che suddivida la parte posteriore del pannello e dimezzi la superficie radiante della faccia posteriore degli altoparlanti montati sullo stesso, potremmo ottenere il nostro scopo in modo semplice ed efficace: la forma del nuovo pannello, visto dall’alto, ci ricorda una T, è nato il T-polo o Tipolo!
A questo punto il teorico funzionamento dovrebbe essere intuitivo: l’emissione frontale raggiunge il bordo del semipannello con una energia maggiore di quella posteriore, dato che la superficie radiante anteriore è doppia rispetto a quella posteriore, avendo quest’ultima l’altra metà schermata dal pannello.
Ma, ovviamente c’è sempre un ma...
La superficie radiante posteriore viene ora a trovarsi in corrispondenza di almeno due pareti riflettenti, e questo porta a un incremento, non a una riduzione di efficienza. Come si comporta allora una sorgente acustica posta in queste condizioni?
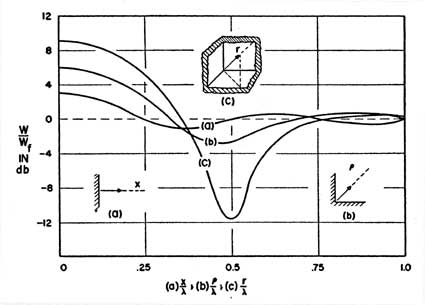
Ci viene in aiuto uno studio di Richard Waterhouse, che illustra proprio una situazione simile alla nostra. L’energia acustica irradiata da sorgente posta nella congiunzione di due pareti riflettenti può essere compreso fra tre e sei dB, allorquando il rapporto p/ non superi il valore di 0,25. Se immaginiamo la sorgente in prossimità della congiungente, meno di 10 cm nel nostro esempio, potremo attenderci un incremento abbastanza costante fino a circa 800Hz, con andamento calante a partire da circa 6 dB a 20 Hz fino a circa 3 dB alla frequenza limite di 800. non superi il valore di 0,25. Se immaginiamo la sorgente in prossimità della congiungente, meno di 10 cm nel nostro esempio, potremo attenderci un incremento abbastanza costante fino a circa 800Hz, con andamento calante a partire da circa 6 dB a 20 Hz fino a circa 3 dB alla frequenza limite di 800.
Infatti  @800Hz=0,43 e p/ @800Hz=0,43 e p/ = 0,1/0,43=0,23 = 0,1/0,43=0,23
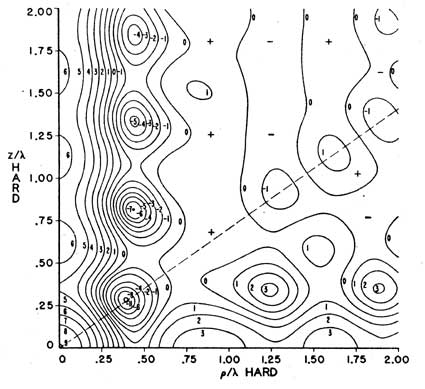
Un successivo lavoro di Waterhouse e Cook (sopra) integra lo studio appena visto con una serie di pattern delle interferenze che si vengono a creare in presenza di pareti riflettenti, siano esse rigide o “morbide”. Prendendo in esame il grafico che mostra i campi di pressione generati nella coincidenza di due pareti verticali e del pavimento, possiamo notare come per l’intero intervallo compreso per un un rapporto p/ = 0÷0,25 il guadagno oscilli tra +3 e +6 dB, con una serie di ventri di pressione che si snodano lungo la verticale. = 0÷0,25 il guadagno oscilli tra +3 e +6 dB, con una serie di ventri di pressione che si snodano lungo la verticale.
Anche considerando la situazione peggiore, cioè il woofer superiore, dato che il suo centro è posto a circa 70cm dal pavimento, il rapporto z/ per la frequenza limite di 800Hz è uguale a 1,62 , per la frequenza limite di 800Hz è uguale a 1,62 ,
infatti  @800Hz=0,43 e z/ @800Hz=0,43 e z/ = 0,7/0,43=1,62 = 0,7/0,43=1,62
Quindi, data la costanza di pressione lungo la congiungente dei piani, la sorgente rimane comunque a giacere in zona di relativa uniformità.
Ma nel calcolo totale della potenza irradiata noi dobbiamo fare i conti con la complessità della situazione, che vede, rispetto alla faccia anteriore dell’altoparlante, una Sd dimezzata, con conseguente riduzione della sensibilità media, quindi il computo totale potrebbe portare a un incremento molto meno sensibile e considerabile di una certo interesse solo al disopra di un rapporto p/ =0,12, cosa che limita l’efficacia della paratia ai 400 Hz e con solo 2 o 3 dB di differenziale nei confronti del livello irradiato dalla faccia anteriore del dipolo. =0,12, cosa che limita l’efficacia della paratia ai 400 Hz e con solo 2 o 3 dB di differenziale nei confronti del livello irradiato dalla faccia anteriore del dipolo.
C’è però da considerare anche che le due emissioni posteriori devono compiere un tragitto più lungo per ricongiungersi all’emissione anteriore, quindi la paratia posteriore ha anche la funzione di prolungare il pannello e abbassare la Fc del sistema di qualche Herz. La paratia ha anche un’altra funzione, ma questa sarà molto evidente in fase di misura e la vedremo in quella sede.
Naturalmente la massima efficacia la si otterrebbe con una paratia di dimensioni tendenti all’infinito, ma già con una misura paragonabile al semipannello stesso l’effetto dovrebbe essere avvertibile, senza contare che la lunghezza può essere poi facilmente incrementata semplicemente aggiungendo delle porzioni, o realizzandola a “soffietto”, in modo da contenere l’ingombro del Tipolo quando non è in uso.
Una variante interessante del sistema potrebbebbe poi essere l’utilizzo di due driver separati che vedono le loro superfici radianti sommarsi solo sulla faccia anteriore del pannello, mentre posteriormente la paratia a T divide a metà la Sd risultante. Questo espediente, ovviamente, può essere utilizzato solo con altoparlanti di piccolo diametro (8” - 10”), altrimenti la larghezza del pannello diverrebbe esagerata; per raggiungere una Sd sufficiente e una Vas adeguata si potrebbero usare quattro 10” montati in quadrato e separati dalla paratia in due coppie in verticale.
MA FUNZIONA?
Alla luce di quanto visto sopra, il consiglio è quello di sfruttare il Tipolo solo in bassa frequenza, tipicamente sotto i 500 Hz, mentre l’uso con un largabanda può portare qualche problema.
Le misure sul prototipo del tipolo, il “prototipolo”
Non è facile effettuare misure in bassa frequenza in assenza di camera anecoica.
Per ovviare a questo ho utilizzato la tecnica di misurazione Ground Plane, che prevede il posizionamento a pavimento sia del sistema che del microfono. La tecnica, ottimamente illustrata da Mark Gander, fornisce risultati attendibili , se non proprio in senso assoluto, almeno comparativi, dato che i sistemi con e senza la paratia posteriore sono stati misurati esattamente nelle stesse condizioni. La misurazione è stata effettuata su un prototipo utilizzante un woofer Macrom da 250 mm con Qt .9 e Fs 40 Hz, il pannello era di soli 45 cm e la paratia posteriore da 50, questo perchè la Ft risultante non sarebbe stata troppo bassa, cosa che avrebbe complicato ancor più l’effettuazione delle misure. Seppure di non grande entità, è comunque evidente una maggiore estensione in basso del sistema Tipolo, comparato allo stesso pannello in mancanza della paratia posteriore. evidente anche l’alterazione alle frequenze superiori dovute all’emissione su 1/8 di spazio della faccia posteriore della membrana. La misura di Waterfall e di ETC mostra in parte cosa avviene, con una maggore “tenuta” delle basse frequenze, che vanno a spegnersi con una maggiore lentezza, pur giungendo alla stessa attenuazione nello stesso arco di tempo.
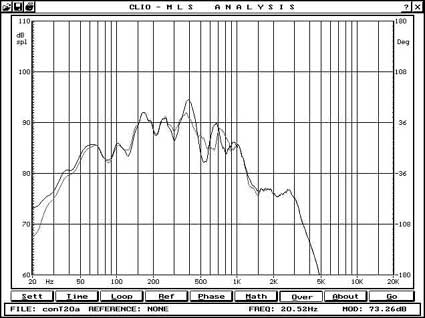
Risposta del dipolo con e senza la paratia
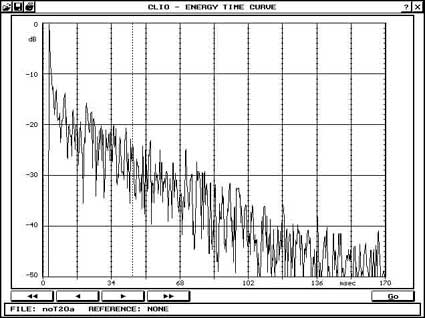 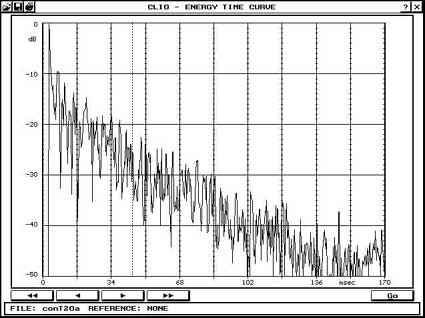
ETC senza (in alto) e con la paratia (sopra)
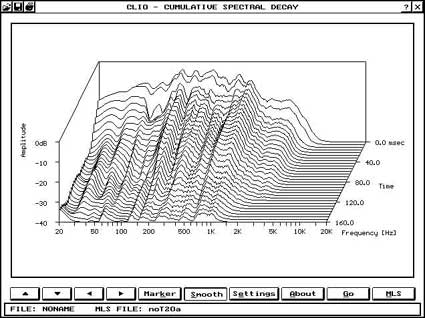 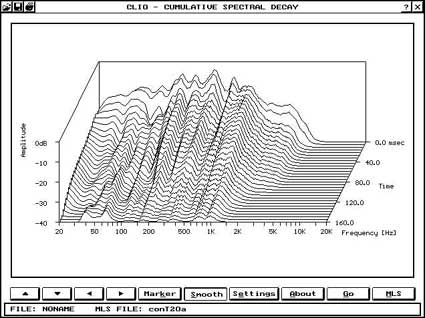
Waterfall senza (in alto) e con la paratia (sopra)
Sulla base di quanto sopra illustrato, è stato realizzato un sistema a Tipolo. Il progetto è stato inviato al concorso CIARE per autocostruttori. Esaurita la fase del concorso verranno illustrati i particolari del progetto.
Grazie dell'attenzione
Filippo Punzo
REFERENCE
Harry Olson - “Gradient Loudspeakers”, JAES vol. 21 n°2, march 1973
Siegfried Linkwitz - “Models for a dipole loudspeaker design”, http://www.linkwitzlab.com/models.htm
Raymond Newman - “Dipole Radiator System”, JAES vol. 28 n°1/2, jan./feb. 1980
Daniele Coen - “Hi-end fai da te, il dipolo Audax-Res”, Audio Review n°150, giugno 1995
Edward Jones - “Providing foldback with out-of-phase loudspeakers”, JAES vol. 19 n°4, april 1971
John Hilliard - “Unbaffled speakers column array”, JAES vol. 18 n°6 dec. 1970
Chester Rice e Edward Kellogg - “Notes on the development of a new type of hornless loudspeakers”, AIEE vol.44 sept. 1925
Richard Small - “Direct radiator loudspeaker system analysis” JAES vol. 20 n°5, june 1972
D.B. Keele - “Low-frequency loudspeakers assement by nearfield sound-pressure measurement”, JAES vol. 22 n°3, april 1974
D.B. Keele - “Direct low-frequency driver synthesis from system specifications”, JAES vol. 30 n°11, nov. 1982
Jason Christophorou - "Low-frequency loudspeaker measurements with an accelerometer”, JAES vol. 28 n°11, nov. 1980
Mark Gander - “Ground-plane acoustic measurement of loudspeakers systems”, JAES vol. 30 n°10, oct. 198
Richard Waterhouse - “Output of a sound source in a reverberation chamber and other reflecting environment”, JASA vol.30, jan. 1958
Richard Waterhouse e Richard Cook - “Interference pattern in reverberant sound field II”, JASA vol.37, march 1965
Keith Ballagh - “Optimum loudspeaker placement near reflecting planes”, JAES vol. 31 n°12, dec. 1983
Roy Allison - “The influence of room boundaries on loudspeakers power output”, JAES vol. 22 n°5, june 1974
Benjamin Bauer - “Broadening the area of stereophonic perception”, JAES vol. 8 n°2, april 1960
|
|

